Question

Which equation represents an exponential function that passes through the point (2, 36)?

Answer 1

In order to be an exponential function, the Xvariable has to be in the exponent, that eliminatesthe second and fourth answers f(X) = 4(3)X using the point (2,36) f(2) = 4 (3)2 = 4 (9 ) = 36

Answer 2

`y=6^x` and
`y=(-6)^x`

Explanation:

Here are given a point (2,36) and find out the exponential function which passes through this point.

In order to do so , we first check the standard form of an exponential form.

The standard form is given as

`y=a^x`

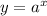
Now if point (2,36) lies on graph of this function , it must satisfies the equation of function . Hence let us substitute x=2 and y = 36 in our standard form.

`36=a^2`

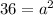
Now taking square roots on each sides we get

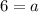`6=a` and
`-6=a`

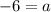
Hence our exponential functions are

`y=6^x` and
`y=(-6)^x`