Answer:
Option D is correct.
No, the triangles are not similar.
Explanation:
AA postulates states that two triangles are similar if they have two corresponding angles equal.
Labelled the diagram as shown below:
We know that sum of all the measure of the angles in a triangle is 180 degree.
In triangle ABC:
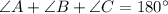
⇒
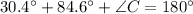
⇒
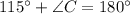
Subtract 115 degree from both sides we get;
⇒
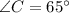
In triangle ABC and PQR
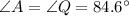
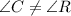
i.e
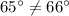
⇒These triangles does not satisfy the AA postulates
Therefore, the given triangles are not similar.