Question

Show that it is not possible for the lengths of the

segments of two intersecting chords to be four consecutive
integers

Answer 1

1. Check the picture below.

2. By the well known intersecting secants property: AO*OC=BO*OD

3. Since the segments are assumed to be consecutive integers, AO, OC cannot be the smaller, and neither can AO<BO and OC<OD.
The only possibility is that the multiplication of the smallest to the largest is equal to the multiplication of the middle 2.

4. For example : 4*5=2*10, we must have 4>2 but 5<10

Here the ordering is 2<4<5<10, similarly assume BO<AO<CO<DO

5. since the segments are of consecutive integers length, let them be

BO=n, AO=n+1, CO=n+2, DO=n+3

6. AO*CO=BO*DO

so n(n+3)=(n+1)(n+2)

`n^(2)+3n= n^(2)+3n+3`
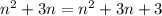
so 0=3 which makes no sense, so no solution with the assumed conditions.