Question

A person invested $20,000 into two accounts that pays 2.5% and 3% simple interest annually, respectively. find the amount invested into the two accounts if the total interest earned after one year is $540

Answer 1

Answer: The amount invested in first account is $12,000 and in second account is $8000

Step-by-step explanation:

We are given:

Total amount invested = $20,000

Total interest earned = $540

Let the amount invested in account 1 having 2.5 % ROI be 'x'

So, the amount invested in account 2 having 3 % ROI will be (20,000-x)

To calculate the simple interest, we use the equation:

`A=(PRT)/(100)`

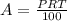
For account 1: For account 2:

P = x P = 20,000 - x

R = 2.5 % R = 3 %

T = 1 T = 1

Putting values in above equation, we get:

`(x* 2.5* 1)/(100)+((20000-x)* 3* 1)/(100)=540\\\\0.025x+600-0.03x=540\\\\x=12000`

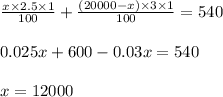
Amount invested in account 1 having 2.5 % ROI = x = $12000

Amount invested in account 2 having 3 % ROI = (20,000 - x) = (20,000 - 12,000) = $8000

Hence, the amount invested in first account is $12,000 and in second account is $8000

Answer 2

Let:
x = amount in the account invested in 2.5%
20000 - x = amount in the account invested in 3%

Solution:
.025x + .03 (20000 - x) = 540
.025x + 600 - .03x = 540
-.005x + 600 = 540
-.005x = 540 - 600
-.005x = -60
x = 12000

Therefore, that person invests 12,000 at 2.5%
and
20,000 - 12,000 = 8,000 at 3%