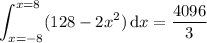Because the height and base of each cross section are equal, the area for any given cross section is
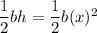
where the base of each section occurring along the line
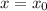
is the vertical distance between the upper and lower halves of the circle
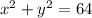
.
We can write
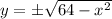
so that
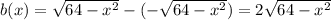
and so the area of each cross section is

Over the circular base of the solid, we have
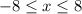
, so the volume of the solid is given by the integral