Answer:
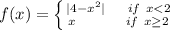
A is correct
Explanation:
The given graph break at point x=2. It would be piece wise function.
- For left side of x=2, graphs is parabolic and y is always positive.
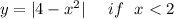
- For right side of x=2, graphs is straight line and slope is positive.
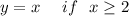
Now we write as piece wise function.
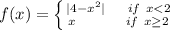
The given graph is combination o parabola and straight line which breaks at x=2