Answer:
The required function is
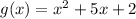 .
.
Explanation:
The given function is
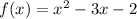
The transformation of a function is defied as
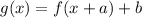
Where a is horizontal shift and b is the vertical shift.
If a>0, then the graph of f(x) shifts a units left and if a<0, then the graph of f(x) shifts a units right.
Since the graph of f(x) shifts 4 units left, therefore a=4.
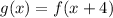

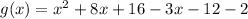
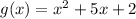
Therefore the required function is
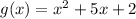 .
.