Question

Which set of values could be the side lengths of a 30-60-90 triangle?

Answer 1

If we say that side "a" is the shortest (adjacent), side "b" is the second shortest (opposite), and side "c" is the longest (hypotenuse): then angle A would be 30°, angle B would be 60°, and angle C would be 90°

tan B = b/a
or
a tan B = b

they have 4 as the smallest value in all four options, so we know that a=4

4 tan 60° = b
tan 60° = √3
so, 4 tan 60° = 4√3
b=4√3

that leaves two options left, so now we find "c":

c^2 = (a^2) + (b^2)
OR

`c= \sqrt{a^(2) + b^(2)}`


`c= \sqrt{4^(2)+(4√(3))^(2)}`


`c= √(16+48) \\ c=√(64) \\ c=8`

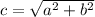
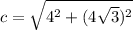
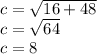
so a=4, b=4√3, and c=8

Making your answer B

Answer 2

A triangle with 30°, 60° & 90° angles is called a semi equilateral triangle.

In such a triangle the hypotenuse equal the side of the equilateral triangle, and the opposite side to the angle 30° is equal half the side of the equilateral or half the hypotenuse.

Assume the side equal 8 & the other 8/2 = 4. let's calculate the 3rd side by applying Pythagoras:

8² = 4² + x² ; 64 = 16 + x² or x² = 64-16 ; x² =48 and
x =√48 = √16. 3 = 4√3

So the 3 sides are 8, 4 and 4√3 (answer B)