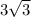Question

What is the length of the altitude of the equilateral triangle below?

Answer 1

its C

h=
`( a*√(3) )/(2)`

Answer 2

The length of the altitude of the equilateral triangle is
`3\sqrt3`

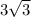
Solution-

The given triangle is an equilateral triangle.

Here, a is a median which bisects the base. It also serves as an altitude, as it is an equilateral triangle.

As the triangle can be divided into two right angle triangle, so applying Pythagoras Theorem,

`\Rightarrow 3^2+a^2=6^2`

`\Rightarrow a^2=6^2-3^2`

`\Rightarrow a^2=36-9`

`\Rightarrow a^2=27`

`\Rightarrow a=√(27)`

`\Rightarrow a=3\sqrt3`

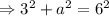
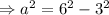
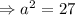
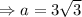
Therefore, the length of the altitude of the equilateral triangle is
`3\sqrt3`