Answer:
The volume increased 27 times of its original value.
Explanation:
Firstly, i have attached an image that it represents the form of a triangular prism.
So, if we use the same variables from the image, the values of each one are:
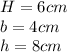
In order to determine the volume of a triangular prism, we need to determine the area of the triangular face of the triangular prism.
The area of the triangular face is:
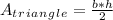
Then, the area of the triangular face is multiplying by the length of the triangular prism, H, to get its volume:

If all dimensions are tripled, the new volume is:
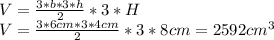
Finally, if we divide the new volumen by the original volume, the value is:
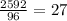
It means that the original volume increased 27 times.