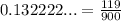Question

Convert into p/q form a) 2.345 b. 6.2525… c. 0.132222…..
plss answer fast!!

Answer 1

a.) To convert a non-repeating decimal into a fraction, we divide the decimal number (without the decimal point) by a power of 10 corresponding to the number of digits after the decimal point and then reduce the resulting fraction to its lowest term.
i.e.

`2.345= (2345)/(10^3) =(2345)/(1000)=(2345 / 5)/(1000 / 5)=(469)/(200)`

b.) To convert a repeating decimal number into fraction we follow the following steps.

Step 1: form an equation with the decimal number you want to convert.
i.e.
`x=6.2525`

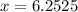
Step 2: move the decimal point to the position after the repeating digit by multiplying both sides of the equation with a power of 10 corresponding to the number of places the decimal point moved.
i.e. here, the repeating digits are 25 and the decimal point will move two places to get to the position after 5. Thus both sides will be multiplied by 100
`(10^2)`
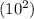
Thus,
`100x=625.2525`

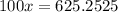
Step 3: move the decimal point to the position before the repeating digit by multiplying both sides of the equation with a power of 10 corresponding to the number of places the decimal point moved.
i.e. here, the repeating digits are 25 and the decimal point is already in the position before 2 from the equation in step 1.
Thus,
`x=6.2525`

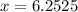
Step 4: Subtract the equation resulting from step 3 from the equation resulting from step 2.
i.e.

`100x=625.2525 \\ -x=6.2525 \\ \\ \Rightarrow 99x=619 \\ \Rightarrow x= (619)/(99)`
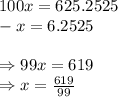
Therefore,
`6.2525... = (619)/(99)`

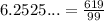
c.) Simillarly, to convert 0.132222 to fraction we follow the following steps.

Step 1: form an equation with the decimal number you want to convert.
i.e.
`x=0.132222`

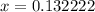
Step 2: move the decimal point to the position after the repeating digit by multiplying both sides of the equation with a power of 10 corresponding to the number of places the decimal point moved.
i.e. here, the repeating digit is 2 and the decimal point will move three places to get to the position after 2. Thus both sides will be multiplied by 1000
`(10^3)`
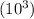
Thus,
`1000x=132.2222`

Step 3: move the decimal point to the position before the repeating digit by multiplying both sides of the equation with a power of 10 corresponding to the number of places the decimal point moved.
i.e. here, the repeating digit is 2 and the decimal point will move two places to get to the position before 2 from the equation in step 1. Thus, we multiply both sides by 100.
i.e,
`100x=13.2222`

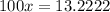
Step 4: Subtract the equation resulting from step 3 from the equation resulting from step 2.
i.e.

`1000x=132.2222 \\ -100x=13.2222 \\ \\ \Rightarrow 900x=119 \\ \Rightarrow x= (119)/(900)`
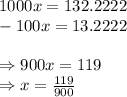
Therefore,
`0.132222... = (119)/(900)`