Question

When 2251 voters were polled, 52% said they were voting yes on an initiative measure. find the margin of error and an interval that is likely to contain the true population proportion. ±2.1%; between 49.9% and 54.1% ±21%; between 31% and 73% ±4.7%; between 47.3% and 56.7% ±47.4%; between 4.6% and 99.4%?

Answer 1

The margin of error for a sample proportion is given by

`z_(\alpha/2)\sqrt{ (p(1-p))/(n) }`
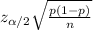
where:
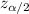
`z_(\alpha/2)` is the z score associated with the confidence level, p is the sample prortion and n is the sample size.
We assume a confidence level of 95%, then
`z_(\alpha/2)=1.96`
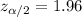
p = 52% = 0.52 and n = 2251

Therefore, margin of error =

`z_(\alpha/2)\sqrt{ (p(1-p))/(n) }= 1.96* \sqrt{ (0.52(1-0.52))/(2251) } \\ = 1.96* \sqrt{ (0.52(0.48))/(2251) } = 1.96* \sqrt{ (0.2496)/(2251) } \\ = 1.96* √(0.000110884) =1.96* 0.0105 \\ =0.0206=2.1\%`

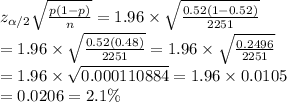
The the interval that is likely to contain the true population proportion is between 49.9% and 54.1%.