Question

While running, a person dissipates about 0.60 j of mechanical energy per step per kilogram of body mass. if a 51-kg person develops a power of 67 w during a race, how fast is the person running? (assume a running step is 1.5 m long.)?

Answer 1

Given: 0.6J/1.5m/kg
For the particular person, since he is 51kg, every step he ran would yield 30.6J
67 W = 67J/S
Time= 30.6J / 67J/s = 0.4567164179s
Speed = 1.5m / 0.4567164179s
= 3.28m/s

Answer 2

The speed of the person is 3.27 m/s.

Step-by-step explanation:

Given that,

Mass of runner = 51 kg

Power = 67 W

Energy = 0.60 J

1 step = 1.5 m

We need to calculate the dissipates energy for 51 kg runner

`\Delta E_(step)= 0.60*51`

`\Delta E_(step)=30.6\ J`

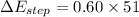
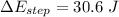
We need to calculate the total energy

Using formula of total energy

`\Delta E_(total)=\Delta E_(step)* S`

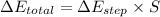
The power is,

`P_(avg)=(\Delta E_(total))/(\Delta t)`

Put the value of
`\Delta E_(total)`

`P_(avg)=(\Delta E_(step)* S)/(\Delta t)`

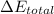
Multiply each side by
`(1)/(E_(step))`

`(P_(avg))/(E_(step))=(S)/(\Delta t)`

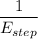
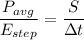
Put the value into the formula

`(S)/(\Delta t)=(67)/(30.6)`

`(S)/(\Delta t)=2.18`

`S=2.18\Delta t`

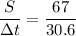
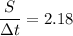
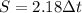
We need to calculate the speed of the person

Using formula of speed

`v =(d)/(t)`

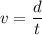
Here,
`d = S*1.5`

`v=(S*1.5)/(\Delta t)`

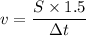
Where, d = distance

t = time

Put the value into the formula

`v=(2.18*\Delta t*1.5)/(\Delta t)`

`v= 2.18*1.5`

`v=3.27\ m/s`

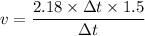
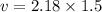
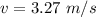
Hence, The speed of the person is 3.27 m/s.