Question

Abigail and Bailey wash dogs to make extra money. Abigail can wash all of the dogs in 5 hours. Bailey can wash all the dogs in 3 hours. How long will it take them to wash the dogs if they work together?

a.1/15 hours
b.1 7/8 hours
c.8/15 hours
d.1/8 hours

Answer 1

Answer: The correct option is (b)
`1(7)/(8)~\textup{hours}.`

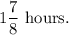
Step-by-step explanation: Given that Abigail and Bailey wash dogs to make extra money. Abigail can wash all of the dogs in 5 hours and Bailey can wash all the dogs in 3 hours.

We are to find the time taken by them if they wash the dogs together.

Abigail can wash the dogs in 5 hours.

So, in 1 hour, the fraction of the dogs Abigail can wash is given by

`(1)/(5).`

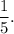
Bailey can wash the dogs in 3 hours.

So, in 1 hour, the fraction of the dogs Bailey can wash is given by

`(1)/(3).`

Hence, if they work together, then the fraction of the dogs that they wash in 1 hour is given by

`(1)/(5)+(1)/(3)=(3+5)/(15)=(8)/(15).`

Therefore, the time taken by them to wash the dogs if they work together will be

`t=(1)/((8)/(15))=(15)/(8)=1(7)/(8)~\textup{hours}.`

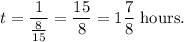
Thus, option (b) is correct.