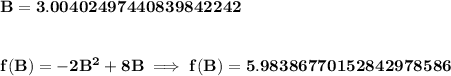Question

an arch way is modeled by the equation y=-2x^2+8x. A rod is to be placed across the archway at an angle definded by the equation x-2.23y+10.34=0. If the rod is attached to the archway at points A and B, such that point B is at a higher level than point A, at what distance from the ground is point B ?

Answer 1

so.. hmm check the picture below

now, to know where A and B are, that occurs when the parabolic equation equates the linear one

thus


`\bf y=-2x^2+8x \\\\\\ x-2.23y+10.34=0\implies \cfrac{x+10.34}{2.23}=y \\\\\\ y=y\implies -2x^2+8x=\cfrac{x+10.34}{2.23} \\\\\\ -4.46x^2+17.84x=x+10.34 \\\\\\ 0=4.46x^2-16.84x+10.34`

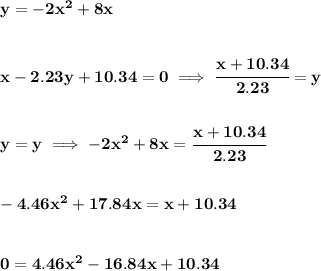
now, running that on the quadratic formula, you end up with the values of 3.00402497440839842242 and 0.77175977895483027713

thus B rounded up is 3.004 and A rounded up is 0.7718

what's the "y" value for B?, well, you can use either the linear or quadratic equation for that, let's use the quadratic one


`\bf B=3.00402497440839842242 \\\\\\ f(B)=-2B^2+8B\implies f(B)=5.98386770152842978586`