According to the general equation for conditional probability, if P(A^B)= 3/10 and P(B)= 2/5 what is P(A|B)?

Question

asked Feb 27, 2018 26.4k views

2 Answers

Srivani · Answer 1 · 2018-02-27T22:01:06+0000

Answer:

P(A/B)=
{(3)/(4)}

Explanation:

According to the general equation for conditional probability, if P(A^B)= 3/10 and P(B)= 2/5

P(A∩B) = 3/10

P(B)= 2/5

We need to find P(A/B)

the formula is P(A/B) = P(A∩B)/ P(B)

Plug in the given values

P(A/B)=
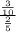
((3)/(10) )/((2)/(5) )

P(A/B)=
{(3)/(10) * {(5)/(2)

P(A/B)=
{(3)/(4)}