Answer:
A. 10.8.
Explanation:
We are given that a shape ABCD . The point A is (7,5), B (6,3), C(3,2) and D (4,4).
By using distance formula we find sides of given shape and then find perimeter.
Distance formula:The distance between two points
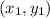 and
and
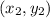
=
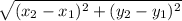
Length of side AB=
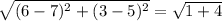
Length of side AB=
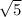 units
units
Length of BC=
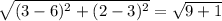
Length of side BC=
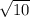 units
units
Length of side CD=
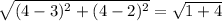
Length of side CD=
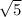
Length of side AD=
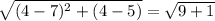
Length of side AD=
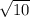
Therefore, the perimeter of given shape ABCD=AB+BC+CD+AD
The perimeter of given shape ABCD=
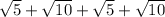
The perimeter of given shape ABCD=
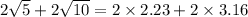 .
.
Substitute
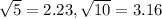
The perimeter of given shape=4.46+6.32
The perimeter of given shape=10.78=10.8(round off)
Hence, the perimeter of given shape=10.8 units
Therefore, option A is correct.