Question

A fourth degree polynomial that has five terms could have five linear factors.

Answer 1

This is false. The most it could have is 4

Answer 2

Answer with explanation:

Fourth degree Polynomial that has five terms

`x^4+ax^3 +bx^2+c x+d`

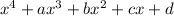
It will have maximum of four linear factors.

which can be written as =(m x-p)(n x-q)(w x-r)(t x-s)

Because a Polynomial of Degree four has maximum of four Zeroes.So, there will be four linear factors of a Fourth degree Polynomial.

For example :

Consider a Quadratic Polynomial

1. x²-3 x +2=(x-1)(x-2)

has two linear Factors.

⇒2. Cubic Polynomial

x³-x²-x+1

=x²(x-1)-1(x-1)

=(x²-1)(x-1)

=(x-1)(x+1)(x-1)

Three Linear Factors

⇒Similarly, a fourth degree polynomial having either five terms or more than five terms will have only four linear factors.

⇒≡The Given Statement is false: A fourth degree polynomial that has five terms could have five linear factors.