Question

If u(x)=-2x^2 + 3 and v(x)=1/x, what is the range of (u*v)(x)?

Answer 1

u(x) = 2x² + 3 and v(x) = 1/x


1st find u(v(x)):[Replace x of v(x) by the x of u(x)

u(x) = 2.(1/x)² + 3 === u(x) = 2x² +3

This s a parabola (open downward) with a minimum at (0,3)

So the range is {y/y≥ +3)

Answer 2

All negative real numbers.

Explanation:

We have been given two function

`u(x)=-2x^2+3`

`v(x)=(1)/(x)`

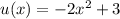
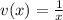
First, we need to compute (u*v(x)) it means we have to put v(x) in place of x in u(x) then only it will become u(v(x))

`u((1)/(x))=-2(1)/(x^2)+3=-2x^2`

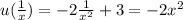
Range is the value here y that is f(x) will take

All negative real numbers