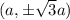Question

In equilateral triangle RST, R has coordinates (0, 0) and T has coordinates of (2a, 0). Find the coordinates of S in terms of a.

Answer 1

the x coordinate of S will be 1/2 * 2a = a.
and since the half triangle is 30-60-90 the y coordinate will be sqrt3 a

so S is (a , sqrt3a)

Answer 2

The S coordinate :

`(a,√(3)a)\text{ and }(a,-√(3)a)`

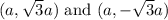
Explanation:

In equilateral triangle RST, R has coordinates (0, 0) and T has coordinates of (2a, 0)

We need to find the third coordinate of triangle RST.

R(0,0)

T(2a,0)

S(x,y)

RT=RS=ST (because RST is an equilateral triangle)

Using distance formula,

`√(x^2+y^2)=√((x-2a)^2+y^2)=2a`

`√(x^2+y^2)=√((x-2a)^2+y^2)`

`x^2=(x-2a)^2`

`x^2=x^2+4a^2-4ax`

`x=a`

`√(x^2+y^2)=2a`

`x^2+y^2=4a^2`

`y^2=4a^2-a^2=3a^2`

`y^2=3a^2`

`y=\pm √(3)a`

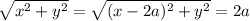
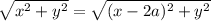
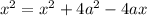
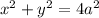
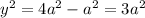
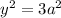
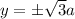
Hence, The S coordinate :
`(a,\pm √(3)a)`