Question

The mean of a normally distributed dataset is 12, and the standard deviation is 2.

% of the data points lies between 8 and 16.

Answer 1

NormalCdf(-2,2,0,1)=.9545
95.45%

Answer 2

95.44% of the data lies between 8 and 16.

Explanation:

Since, z score or standard score formula is,

`z=(x-\mu)/(\sigma)`

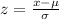
Where,

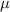`\mu` = mean of the data,

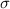`\sigma` = standard deviation,

Let X represents a data point,

So, we have to find out,

P( 8 < X < 16),

Since,

`P(8 < X < 16)=P((8-\mu)/(\sigma)< Z< (16-\mu)/(\sigma))`

`=P((8-12)/(2)<Z<(16-12)/(2))`

`=P(-2<Z<2)`

`=P(Z<2) - P(Z<-2)`

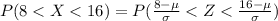
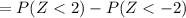
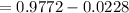`=0.9772-0.0228` ( By the z-score table )

`=0.9544`

`=95.44\%`

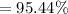
Hence, 95.44% of the data lies between 8 and 16.