Question

5^n+1+4.6^n whwn divide by 20 leaves remainder 9 prove by mathematical induction

Answer 1

hello here is a solution : 

Answer 2

It is true for all values if n

Explanation:

Let

`P(n)=5^(n+1)+4.6^(n)-9`

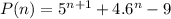
We have to prove that 20 is a factor of P(n) by mathematical induction.

Let us start:

Step1:

Check P(n) is true for 1.

`P(1)=5^(1+1)+4.6^(1)-9\\P(1)=5^(2)+4.6^(1)-9\\P(1)=25+24-9\\P(1)=40=20*2`

Hence P(n) is true for n=1

Step 2:

Assume that P(n) is true for some value of n say t

That is P(t) is true or

`5^(t+1)+4.6^(t)-9=20k`

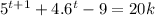
Where k is some constant…

Step3:

We have to prove that P(t+1) is also true, then P(n) is true for every value of n.

Hence

`P(t+1)= 5^((t+1+1))+4*6^(t+1)-9`

`P(t+1)=5^(t+1)*5+4*6^t*6-9\\=5^(t+1)*5+4*6^t*(5+1)-9\\=5^(t+1)*5+(4*6^t)*5+(4*6^t) -9\\=5(5^(t+1)+4*6^t)+(4*6^t) -9\\=5(20k+9)+ 4*6^t -9\\=100k+45-9+4*6^(t)\\=100k+36+4*6^(t)\\=100k+4(9+*6^(t))\\=100k+4(20k-5^(t+1))\\=100k+80k-4*5*5^t\\=180k-20*5^t\\=20(9k-5^t)\\=20r`

where r is some constant.

Hence

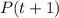`P(t+1)` is also true ,

Thus P(n) is true for all values of n , and we can say that

When
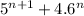`5^(n+1)+4.6^(n)` is divided by 20, we get 9 as remainder.