Question

Abcd is a parallelogram. its diagonal, ac, is 18 inches long and forms a 20° angle with the base of the parallelogram. angle abc is 130°. what is the length of the parallelogram's base, ab?

Answer 1

i really need this answer

Answer 2

The length of base of parallelogram, AB = 11.75 in

Explanation:

ABCD is a parallelogram. Its diagonal, AC, is 18 inches long and forms a 20° angle with the base of the parallelogram. Angle ABC is 130°

Please see attachment.

In ΔABC

∠A+∠B+∠C=180° (Angle sum property of triangle)

20°+130°+∠C=180° (∴ ∠A=20° , ∠B=130° )

∠C=30°

Using sine law:

`(\sin C)/(c)=(\sin A)/(a)=(\sin B)/(b)`

where, ∠C=30°, c=AB=? , b=18 , ∠B=130°

Substitute into formula

`(\sin 30^\circ)/(AB)=(\sin 130^\circ)/(18)`

`AB=(18\cdot \sin 30^\cric)/(\sin 130^\circ)`

`AB=(18\cdot 0.5)/(0.766)`

`AB=11.75\text{ in}`

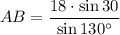
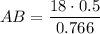
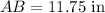
Hence, The length of base of parallelogram, AB = 11.75 in