Question

The length of a screw produced by a machine is normally distributed with a mean of 0.75 inches and a standard deviation of 0.01 inches. what percent of screws are between 0.72 and 0.78 inches? (1 point 68% 75% 99.7% 100%

Answer 1

99.7%
You can use normalCdf(.72,.78,.75,.01) to find the answer or if you standardize your numbers (z scores) normalCdf(-3,3,0,1).

Answer 2

Answer: There is 99.7% of screws are between 0.72 and 0.78 inches.

Explanation:

Since we have given that

Mean = 0.75 inches

Standard deviation = 0.01 inches

Since the length of a screw produced by a machine is normally distributed.

So, We need to find the percent of screws are between 0.72 and 0.78 inches.

Since we have that

`P(0.72<X<0.78)`

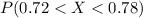
And we know that

`z=(X-\mu)/(\sigma)`

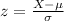
So, it becomes,

`P((0.72-0.75)/(0.01)<z<(0.78-0.75)/(0.01))\\\\=P(-3<z<3)\\\\=2* P(0<z<3)\\\\=2* 0.49865\\\\=0.9973\\\\=0.9973* 100\\\\=99.73\%`

Hence, there is 99.7% of screws are between 0.72 and 0.78 inches.