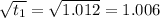Question

Find any relative extrema of the function. (Round your answers to three decimal places.) f(x) = arcsec(x) − 9x

Answer 1

1. Relative extrema of functions are the "tops" or the "bottoms" of the curves (the graphs) representing functions. So they are the points at which the tangent lines are horizontal.

2. In short we are looking for the solutions of f'(x)=0

3. f'(x)=
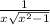
`\frac{1}{x \sqrt{ x^(2) -1} }`-9=0


`x \sqrt{ x^(2) -1}= (1)/(9)`

Notice:
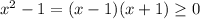
`x^(2) -1 =(x-1)(x+1) \geq 0` so that the square root of this expression exists. So x
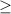
`\geq`1 or x
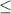
`\leq`-1

Also in
`x \sqrt{ x^(2) -1}= (1)/(9)` notice that the root is always positive and 1/9 is positive, so x must be positive. This second condition, combined with the first one tells us that the solution is in x
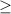
`\geq`1

4.

`x \sqrt{ x^(2) -1}= (1)/(9)`

Square both sides


`x^(2) (x^(2) -1)= (1)/(81)`



`x^(4)-x^(2)- (1)/(81)=0`

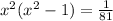
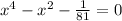
let
`t= x^(2)`
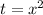
Then the 4th degree equation becomes the quadratic equation


`t^(2)-t- (1)/(81)=0`

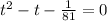
The discriminant D=
`b^(2) -4ac=1-4(- (1)/(81) )=1+ (4)/(81)=1+ 0.049=1.049`

`√(D) = √(1.049) =1.024`


`t_(1)= (-b+ √(D) )/(2a)= (1+1.024)/(2)= (2.024)/(2)= 1.012`


`t_(2)= (-b- √(D) )/(2a)= (1-1.024)/(2)= (-0.024)/(2)= -0.012`


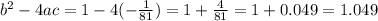
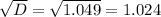
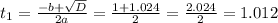
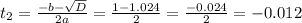
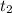
`t_(2)` is not considered as
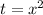
`t= x^(2)` so t cannot be negative

x=
`\sqrt{ t_(1) }= √(1.012)= 1.006`