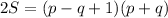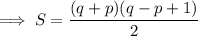Question

Hello everyone, I need help with an exercise about summations, why p + (p + 1) + ... + (q - 1) + q can be resolved bye the equation
`((q+p)(q-p+1))/(2)`.

I just want to know why the summation can be resolved by this equation.

Answer 1

Let
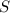
`S` denote the sum in question:


`S=p+(p+1)+\cdots+(q-1)+q`

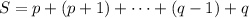
Reorder the terms as


`S=q+(q-1)+\cdots+(p+1)+p`

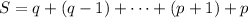
Note that each corresponding term in the sums add to
`p+q`:


`p+q=p+q`

`(p+1)+(q-1)=p+q`
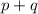
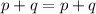
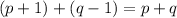
and so on.

So adding both sums together gives


`2S=(p+q)+(p+q)+\cdots+(p+q)+(p+q)`

There are
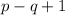
`p-q+1` instances of
`p+q`. (
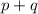
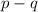
`p-q` is the difference between the first and last terms of the sum, i.e. the number of terms after
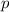
`p` to count up to
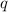
`q`. Adding 1 will include
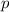
`p` in the count.) So,


`2S=(p-q+1)(p+q)`

`\implies S=\frac{(q+p)(q-p+1)}2`