Question

In circle A shown below, Segment BD is a diameter and the measure of Arc CB is 36°: Points B, C, D lie on Circle A; line segment BD is the diameter of circle A; measure of arc CB is 36 degrees. What is the measure of ∠DBC?

Answer 1

The measure of ∠DBC is 72°.

Explanation:

Given information: BD is a diameter, A is center of circle, Arc CB=36°.

According the angled inscribed in a semicircle theorem, the angle inscribed in a semicircle is a right angle.

`\angle BCD=90^(\circ)`

According to the central angle theorem, the angle inscribed on the circle is half of its central angle.

`\angle BDC=(\angle BAC)/(2)=(36^(\circ))/(2)=18^(\circ)`

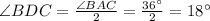
By angle sum property, the sum of interior angles of a triangle is 180 degrees.

`\angle BDC+\angle BCD+\angle DBC=180`

`18^(\circ)+90^(\circ)+\angle CBD=180^(\circ)`

`108^(\circ)+\angle CBD=180^(\circ)`

`\angle CBD=180^(\circ)-108^(\circ)`

`\angle CBD=72^(\circ)`

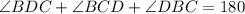
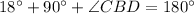
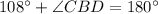
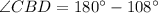
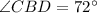
Therefore the measure of ∠DBC is 72°.