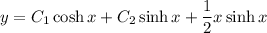Question

Solve this problem by using variation of parameters method.
y''-y=coshx.

Answer 1

`y''-y=0\implies r^2-1=0\implies r=\pm1`

`\implies y_c=C_1e^x+C_2e^(-x)={C^*}_1\underbrace{\cosh x}_(y_1)+{C^*}_2\underbrace{\sinh x}_(y_2)`

For the nonhomogeneous ODE


`y''-y=\underbrace{\cosh x}_(f(x))`

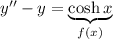
we're looking for a particular solution of the form


`y_p=u_1y_1+u_2y_2`

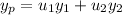
where


`u_1=-\displaystyle\int(y_2(x)f(x))/(W(y_1(x),y_2(x)))\,\mathrm dx`

`u_2=\displaystyle\int(y_1(x)f(x))/(W(y_1(x),y_2(x)))\,\mathrm dx`

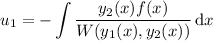
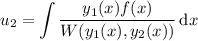
and
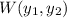
`W(y_1,y_2)` is the Wronskian of the two fundamental solutions.

We have


`W(y_1,y_2)=\begin{vmatrix}\cosh x&\sinh x\\\sinh x&\cosh x\end{vmatrix}=\cosh^2x-\sinh^2x=1`

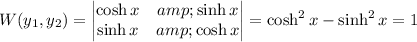
so we're left with


`u_1=-\displaystyle\int\sinh x\cosh x\,\mathrm dx=-\frac12\cosh^2x`

`u_2=\displaystyle\int\cosh^2x\,\mathrm dx=\frac12x+\frac14\sinh2x`

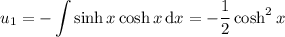
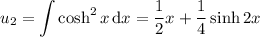
so that the particular solution is


`y_p=-\frac12\cosh^3x+\frac12x\sinh x+\frac14\sinh x\sinh2x`

`y_p=-\frac12\cosh x+\frac12x\sinh x`

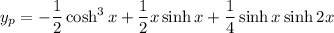
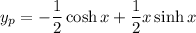
As
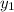
`y_1` already accounts for the
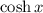
`\cosh x` term in
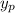
`y_p`, we're left with the general solution


`y=C_1\cosh x+C_2\sinh x+\frac12x\sinh x`