Question

Saturn orbits the Sun at a distance of 1.43 × 1012 m. The mass of the Sun is 1.99 × 1030 kg.

Use to determine Saturn’s orbital period in Earth years. Is it:
A)29.6 Earth years
B)296 Earth years
C)874 Earth years

Answer 1

The answer is A 29.6 Earth Years

Answer 2

Saturn’s orbital period is 29.6 years

Explanation:

It is given that,

The mass of the sun, m = 1.99 × 10³⁰ kg

Saturn orbits the sun at a distance of, a = 1.43 × 10¹² m

Using third law of Kepler's :

`T^2=(4\pi^2)/(GM)a^3`

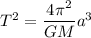
Where,

T is the orbital time period

G is the universal gravitational constant

M is the mass of the sun

a is the distance

So,
`T^2=(4(3.14)^2)/(6.67* 10^(-11)* 1.99* 10^(30))(1.43* 10^(12))^3`

`T=\sqrt{8.688* 10^(17)}\ s`

`T=932094415.818\ s`

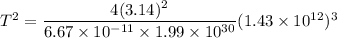
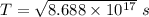
To convert seconds into year divide the time by 3.154 × 10⁷

So, T = 29.55 Years

or T = 29.6 Years

Hence, the Saturn's orbital period is 29.6 Earth years