Question

What is the correlation coefficient with the following data points: (2,47), (3,2), (5,26)?

Answer 1

The correlation coefficient is given by
`\frac{S_(xy)}{\sqrt{S_(xx) S_(yy) } }`


`S_(xy)=`∑
`xy- (∑x)/(n)}` =
`S_(xy)= (2*47)(3*7)(5*26)- ((10*75))/(3)`=


`S_(xx)=(2^(2)+{3^(2)+5^(2))- ((2+3+5)^(2) )/(3) = 34.7`


`S_(yy)=( 47^(2)+2^(2)+26^(2) )`
`- ((47+2+26)^(2) )/(3)`


`S_(xy)`\frac{250}{ \sqrt{34.7+2884} }= 0.79 [/tex]

Answer 2

The correlation coefficient is:

-0.290742

Explanation:

The formula for the correlation coefficient is given by :

`r=\frac{\sum{XY}}{\sqrt{\sum{X^2}\sum{Y^2}}}---------(1)`

where,

`X=x-x'\\and\\Y=y-y'`

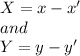
where x' and y' are the mean of x and y entries respectively.

Now,

x y X Y XY X^2 Y^2

2 47 -4/3 22 -88/3 16/9 484

3 2 -1/3 -23 23/3 1/9 529

5 26 5/3 1 5/3 25/9 1

-----------------------------------------------------------------------------------

∑XY= -20

∑X^2=42/9

∑Y^2=1014

( Since,

`x'=(2+3+5)/(3)\\\\x'=(10)/(3)`

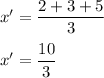
and,

`y'=(47+2+26)/(3)\\\\y'=(75)/(3)\\\\y'=25` )

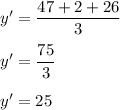Hence,on putting all the values in equation (1) we get:

r= -0.290742