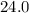Answer:
Area of the given figure is
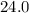
Explanation:
Area of sector of a circle with radius r and central angle
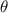
is given by
Area of sector =
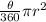
here we have
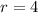
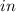
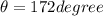
Now we plug the values in the formula
so we have
Area of sector =
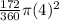
=
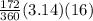
=
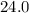
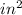
Hence the area of the given figure is