Question

The parabola whose equation is 5x 2 - y = 12 opens

up

down

left

right

Answer 1

5x^2-y=12

y=5x^2-12

dy/dx=10x

d2y/dx2=10

Since acceleration is constant, which is true of all quadratics, and it is positive, there is an absolute minimum for y(x) when dy/dx=0. So it increases without bound on either side of the vertex, meaning that it opens upwards.

Answer 2

The correct option is 1.

Explanation:

In a quadratic equation:

If degree of x is 2 and leading coefficient is negative, then the parabola opens down.

If degree of x is 2 and leading coefficient is positive, then the parabola opens up.

If degree of y is 2 and leading coefficient is negative, then the parabola opens left.

If degree of y is 2 and leading coefficient is positive, then the parabola opens right.

The given function is

`5x^2-y=12`

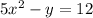
Here, the degree of x is 2 and the leading coefficient is positive, therefore this parabola opens up and the correct option is 1.