** CORRECTIONS: Q1: It's 2x^3-29x+12; Q2,3,4,5,6: All conditions have ≠ symbol; Q7: it's (12x^2+32x+16); Q10: Option D should be divided by x^4; **
(1) Given:
Width = W = x+4
Area = A =
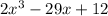
Length = L = ?
Since the pool is rectangular in shape:
area = width * length
A = W * L
Substitute:
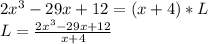
The long division is attached with the answer (below in the picture). Hence the correct answer is
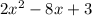 (Option C)
(Option C)
(2) Given expression:
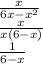
Where x ≠ 6. (Option B)
(3) Given :
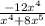
Now simplify:

Where x ≠ -1/8 (Option A)
(4) Given:
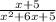
Simplify:
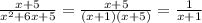
Where x ≠ -1 (Option A)
(5) Given:
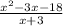
Simplify:
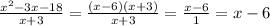 where x≠6 (Option C)
where x≠6 (Option C)
(6) Given:
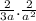
Simplify:
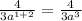
Where a ≠ 0 (Option C)
(7) Mathematically:
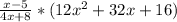
Simplify:
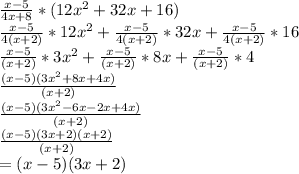
(Option C)
(8) Simplify:
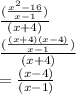
(Option A)
(9) Simplify:
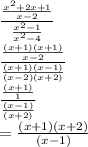
(Option A)
(10) Given:
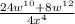
Simplify:
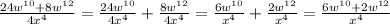
(Option D)
(11) Given:
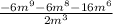
Simplify:
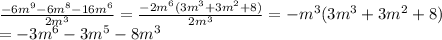
(Option C)
(12) Simplify:
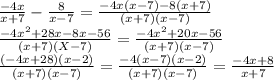
(Option A)
(13) Simplify:
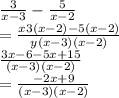
(Option A)
(14) Simplify:
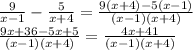
(Option B)
(15) Simplify:
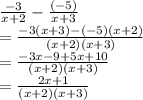
(Option D)
(16) Given:
4/x + 5/x = -3
Simplify:
(4+5)/x = -3
-3x = 9
x = -3 (Option C)
(17) Simplify:
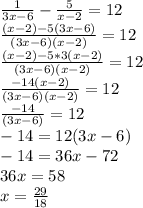
(Option D)
(18) Simplify:
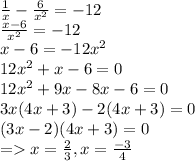
(Option C)
(19) Dorothy's rate (alone) will be:
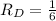
Rosanne's rate (alone) will be:
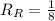
If both work together, add both the rates:
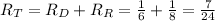 (in 1/hours)
(in 1/hours)
To find the hours, flip the rate:
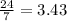 hours (Option B)
hours (Option B)
(20) As pressure (p) is inversely proportional with volume (v):
p = k/v (where k is constant of proportionality)
k = pv
Find constant using initial values:
k = (104)(108)
k = 11232
Now new pressure is:
p = k/v = 11232/432 = 26 Pa (Option A)
(21)
x: 1,3,5,10
y: 4,12,20,40
Direct variation is the value of y increases with x. So,
y = 4x
If x = 1,y=4(1)=4
If x = 3,y=4(3)=12
If x = 5,y=20
If x = 10,y=40 (Option A)
(22)
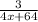
If x=-16,4(-16) + 64 = 0;denominator will become zero,which means that there will be discontinuity at x = -16. Hence, x=-16 (Option C) should be excluded.