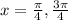Answer:
The asymptotes of
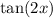 is when
is when
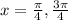
Explanation:
Given :
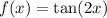 from
from

To find : The asymptotes of the function?
Solution :
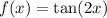
Re-written as
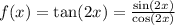
Now, we need to find the value of x that makes
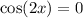
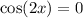
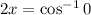

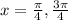
The function
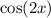 has a period of
has a period of

So, The asymptote of
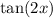 is when
is when
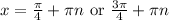
But from

The asymptotes of
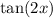 is when
is when