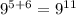Question

How are the power rules for quotients and products similar? How are they different? Refer specifically to the way that the rule is proven to be true.

Answer 1

Power rules for both quotient and product sums are useful to simplify large exponential form (of the same base)

The difference is in the rule. For quotient sum, the powers are subtracted, while for product sum, the powers are added up.

An example for quotient sum

`(7^(13) )/(7^(8) ) = (7*7*7*7*7*7*7*7*7*7*7*7*7)/(7*7*7*7*7*7*7*7*7*7)`
Using the principle of simplifying fractions, we can cancel out ten 7s from both numerator and denominator, leaving us with only three 7s on the numerator which gives us
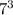
`7^(3)`. This working out could be simplified by doing
`7^(13-10)= 7^(3)`

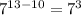
An example for product sum

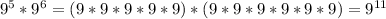
`9^(5)* 9^(6) =(9*9*9*9*9)*(9*9*9*9*9*9)= 9^(11)`. There is a total of eleven 9s if we were to work out the product sum the long way. This could be simplified by doing
`9^(5+6) = 9^(11)`