Question

10. A mountain bike's

suspension works on a
series of springs. What
is the energy stored in
the spring when the
bike goes over a bump
causing a compression
of 2cm. The spring
constant is 33N/m.

Answer 1

The energy stored in the spring when the bike goes over a bump is
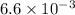`6.6* 10^(-3)` joules.

Step-by-step explanation:

Let suppose that spring has a linear behavious, by means of Hooke's Law, definition of Work and Work-Energy Theorem we find that the potential energy stored in the spring (
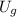`U_(g)`), measured in joules, is defined by:

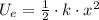`U_(e) = (1)/(2)\cdot k\cdot x^(2)` (1)

Where:

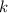`k` - Spring constant, measured in newtons per meter.

`x` - Deformation, measured in meters.

If we know that
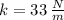`k = 33\,(N)/(m)` and
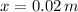`x = 0.02\,m`, the energy stored by the spring due to compression is:

`U_(e) = (1)/(2)\cdot \left(33\,(N)/(m) \right) \cdot (0.02\,m)^(2)`

`U_(e) = 6.6* 10^(-3)\,J`

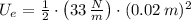
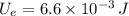
The energy stored in the spring when the bike goes over a bump is
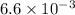`6.6* 10^(-3)` joules.