Question

The terminal side of an angle in standard position passes through P (-3,-4) what is value of tan of theta

Answer 1

The value of tanθ is 4/3.

Step-by-step explanation:

It is given that the terminal side of an angle in standard position passes through P (-3,-4).

We need to find the value of tanθ.

Draw a perpendicular line on the x-axis from the point P(-3,-4).

Let θ is the terminal angle.

In a right angled triangle

`\tan \theta=(opposite)/(adjacent)`

`\tan \theta=(4)/(3)`

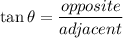
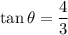
P(-3,-4) lies in 3rd quadrant. The value of tanθ is positive in first and 3rd quadrant.

Therefore, the value of tanθ is 4/3.

Answer 2

The ans is
`(4)/(3)`

The given point is P(-3,-4)

Since x = -3 and y = -4, we find the radius from the origin, r
Then, r =
`\sqrt{( -3)^(2) +(-4 )^(2)}`= 5
Thus, sinФ = y/r = -4/5cosФ = x/r = -3/5
And, tanФ =
`(sinФ)/(cosФ)` =
`(4)/(3)` Ans.