Question

The area of a given hexagon is equal to the area of an equilateral triangle whose perimeter is 36 inches. Find the length of a side of the regular hexagon.The area of a given hexagon is equal to the area of an equilateral triangle whose perimeter is 36 inches. Find the length of a side of the regular hexagon.The area of a given hexagon is equal to the area of an equilateral triangle whose perimeter is 36 inches. Find the length of a side of the regular hexagon. Please answer in square root form.

Answer 1

2squrt6 for short

Answer 2

`\bf \textit{area of an equilateral triangle}\\\\ A=\cfrac{s^2√(3)}{4}\qquad \begin{cases} s=\textit{length of a side}\\ ----------\\ perimeter=s+s+s\\ perimiter=3s\\ 36=3s\\ (36)/(3)=s\\ 12=s \end{cases} \\\\\\ A=\cfrac{12^2√(3)}{4}\implies A=36√(3)`

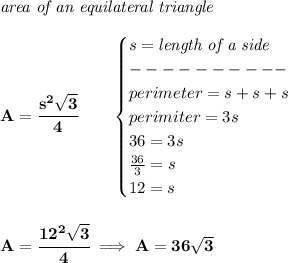
ok.. .based on a side of 12, that's the area of the equilateral triangle, now, the hexagon has the same area... so... let's use the area of a polygon to see what's the length of a side


`\bf \textit{area of a regular polygon}\\\\ A=\cfrac{1}{4}ns^2\ cot\left( (180)/(n) \right)\qquad \begin{cases} n=\textit{number of sides}\\ s=\textit{length of one side}\\ ----------\\ n=6\\ A=36√(3) \end{cases} \\\\\\ 36√(3)=\cfrac{1}{4}\cdot 6\cdot s^2\cdot cot\left( (180)/(6) \right)\implies 36√(3)=\cfrac{1}{4}\cdot 6\cdot s^2\cdot √(3) \\\\\\ 36√(3)=\cfrac{6s^2√(3)}{4}\implies \cfrac{4\cdot 36√(3)}{6√(3)}=s^2 \\\\\\ 24=s^2\implies √(24)=s\implies 2√(6)=s`


now, in case you want to check how much is the cot(30°), check your Unit Circle, recall, cotangent is cosine/sine