so, from 1992 to 1997, it went up by some "r" rate, ok.. that means some percentage, that means some rate of growth, so is an exponential function, with a positive rate, or +r
if we take 1992, to be 0years, then the starting amount for the tuition is 1685
that is
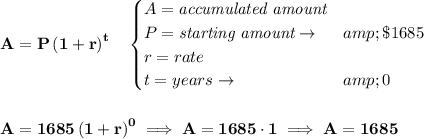
now, let's go to 1997, 5 years later, when t = 5, we know the tuition price then was 2392, so A = 2392
thus
![\bf A=P\left(1+r\right)^t \quad \begin{cases} A=\textit{accumulated amount}\to &\$2392\\ P=\textit{starting amount}\to &\$1685\\ r=rate\\ t=years\to &5 \end{cases} \\\\\\ 2392=1685(1+r)^5\implies \cfrac{2392}{1685}=(1+r)^5\implies \sqrt[5]{\cfrac{2392}{1685}}=1+r \\\\\\ \boxed{\sqrt[5]{\cfrac{2392}{1685}}-1=r}](https://img.qammunity.org/2018/formulas/mathematics/college/zi7gk2q70woq6xex9j0dyi1xvuczwcdgsz.png)
now, you'd get a value in decimal format, so, to get the % format, simply multiply it by 100