Question

You have just inherited $150,261 from a trust that has matured. You would like to invest the total amount into an account that pays you an annual compounded interest rate of 9.1%, and you would like to make annual withdrawals over the next 20 years such that by the end of this 20 year period, the amount remaining in the account will be zero dollars. Determine, from the given information, the amount of the annual withdrawals. Round to the nearest cent.

Answer 1

Hi there
Use the formula of the present value of annuity ordinary and solve for pmt
Pmt=pv÷[(1-(1+r)^(-n))÷r]
PMT=150,261÷((1−(1+0.091)^(−20))÷(0.091))=16,578.03

Hope it helps

Answer 2

$16,574.24

Explanation:

We know the annuity formula is given by,

`P=(r * PV)/(1-(1+r)^(-n) )`

where P = annual payment, PV = present value, r = rate of interest and n = time period.

We have according to the question,

PV = $150,261

r = 9.1% = 0.091

n = 20

Substituting the values in the formula gives us,

`P=(0.091 * 150261)/(1-(1+0.091)^(-20))`

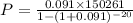
i.e.
`P=(13673.751)/(1-(1.091)^(-20))`

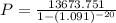
i.e.
`P=(13673.751)/(1-0.175)`

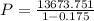
i.e.
`P=(13673.751)/(0.825)`

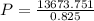
i.e.
`P=16,574.2437`

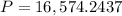
So, the annual withdrawals is of $16,574.2437

After rounding off to nearest cent ( or hundred ), the annual withdrawals is $16,574.24.