Question

Divide the following polynomials and then complete the quotient. Write your answer in order of decreasing powers of x .

(32x^8 - 8x^6 + 28x^4) / 4x^4

Answer 1

Answer: The quotient in order of decreasing powers of x is

`Q=8x^4-2x^2+7.`

Step-by-step explanation: We are given to divide the following polynomials and to complete the quotient :

`Q=(32x^8-8x^6+28x^4)/(4x^4)~~~~~~~~~~~~~~~~~~~(i)`

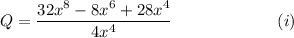
We are to write the answer in order of decreasing powers of x.

From (i), we have

`Q\\\\=(32x^8-8x^6+28x^4)/(4x^4)\\\\\\=(4x^4(8x^4-2x^2+7))/(4x^4)\\\\=8x^4-2x^2+7.`

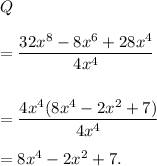
Thus, the required quotient in order of decreasing powers of x is

`Q=8x^4-2x^2+7.`

Answer 2

We need to perform division of polynomials such as the solution is shown below:
( 32x8 - 8x6 + 28x4) / 4x4
(32x8 / 4x4) - ( 8x6 / 4x4 ) + (28x4 / 4x4)
8x4 - 2x2 + 7
The power of the result was already arranged in descending order.

The answer is "8x4 - 2x2 + 7 ".