Question

Bob has 50 feet of fencing to enclose a rectangular garden. If one side of the garden is x feet long, he wants the other side to be (25 – x) feet wide. What value of x will give the largest area, in square feet, for the garden?

Answer 1

this is rather complicated x=(50)^0.5=12.5
let a be area,
a=(25-x) (x)
da/dx=25-2x
dadx=0
25-2x=0
x=12.5

Answer 2

for
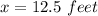`x= 12.5 \ feet` the area will be largest

Explanation:

It is given that one side of rectangular garden is x feet

and other side is 25-x feet

Now the area of the rectangle garden is given by

`A=(25-x)x`

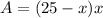
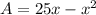`A=25x-x^2` ( we distribute x)

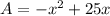`A= -x^2 +25x` ( writing quadratic equation in standard form)

A quadratic function
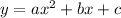`y=ax^2+bx+c` with negative value of a , is a parabola with maximum value at vertex.

the x coordinate of vertex is given by

`x=-(b)/(2a)`

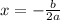
We compare
`-x^2 +25x` with
`ax^2+bx+c`

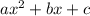
so we have
`a=-1\ b=25\ c=0`

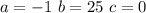
The x coordinate of vertex is given by

`x=-(25)/(2(-1))`

`x=12.5`

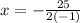
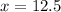
hence for
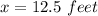`x= 12.5 \ feet` the area will be largest