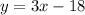Question

Write the point-slope form of the line passing through (2, -12) and parallel to y=3x.

Answer 1

hello :
the line has same slope : y=3x 3 is the slope
the point-slope form is :
y-(-12) = 3(x-2)
y+12 = 3(x-2)

Answer 2

`y = 3x-18`

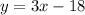
Explanation:

Given :
`y=3x`

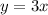
To Find: Write the point-slope form of the line passing through (2, -12) and parallel to y=3x.

Slope of parallel lines are equal .

Standard equation of line :
`y = mx+c`

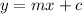
Where m is the slope

So, on comparing with given equation the slope is 3

So, the line parallel to the given line will also have a slope 3

So, the equation of parallel line =
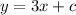`y = 3x+c` --1

Now we are given that this parallel lines passes through (2,-12)

So, substitute (2,-12) in --1

`-12 = 3(2)+c`

`-12 =6+c`

`c=-18`

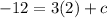
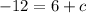
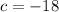
Substitute the value of c in 1

`y = 3x-18`

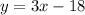
Hence the point-slope form of the line passing through (2, -12) and parallel to y=3x is
`y = 3x-18`