Question

The pentagon is a regular polygon (all sides are equal). What is the Perimeter?

One side is 8x-10
Another side is 2(x+1)

Answer 1

Given:

One side = 8x-10

Another side = 2(x+1)

To find:

The perimeter of the pentagon.

Solution:

We know that, all five sides of a regular pentagon are equal.

`8x-10=2(x+1)`

`8x-10=2x+2`

`8x-2x=10+2`

`6x=12`

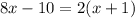
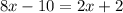
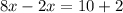
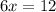
Divide both sides by6.

`x=2`

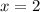
Now, the length of each side of the pentagon is

`Side=8(2)-10`

`Side=16-10`

`Side=6`

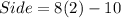
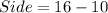
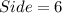
We know that, perimeter of a regular pentagon is

`P=5a`

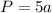
Where, a is the side length.

`P=5(6)`

`P=30`

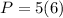
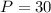
Therefore, the perimeter of the regular pentagon is 30 units.