Question

A parallelogram whose vertices have coordinates R(1, -1), S(6, 1), T(8, 5), and U(3, 3) has a shorter diagonal of ___. 5 √(13) √(97)

Answer 1

Diagonals - across from each other.
This means that S and U are diagonals. Using the distance formula, we deciphered that the length of the diagonal is the square root of 13

Answer 2

A parallelogram whose vertices have coordinates R(1, -1), S(6, 1), T(8, 5), and U(3, 3) has a shorter diagonal of √(13) units.

Explanation:

RSTU is parallelogram. The vertices of the parallelogram are R(1, -1), S(6, 1), T(8, 5), and U(3, 3).

Two opposite vertices are connected by the diagonal of a parallelogram. So, RT and SU are two diagonal.

Distance formula:

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

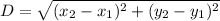
Using this formula we get

`RT=√((8-1)^2+(5+1)^2)=√(49+36)=√(85)`

`SU=√((3-6)^2+(3-5)^2)=√(13)`

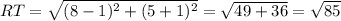
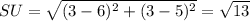
Therefore the parallelogram whose vertices have coordinates R(1, -1), S(6, 1), T(8, 5), and U(3, 3) has a shorter diagonal SU of √(13) units.