Question

Write [2(cos15*+isin15*)]^3 in standard form a+bi

Answer 1

hello :
by moivre theorem :
[2(cos15*+isin15*)]^3 = 2^3(cos(3×45*)+isin(3×45*))
=8 (cos45*+isin45*)
= 8 ( √2/2 +i √2/2)
= 4√2 + 4√2 i ..... ( in standard form a+bi)
a = b = 4√2

Answer 2

Hence, the standard form of the given expression is:

`[2(\cos 15+i\sin 15)]^3=4√(2)+4√(2)i`

Explanation:

We have to represent the expression:

`[2(\cos 15+i\sin 15)]^3` in the standard form:
`a+bi`

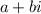
Now, this expression could also be written as:

`[2(\cos 15+i\sin 15)]^3=2^3(\cos 15+i\sin 15)^3`

i.e.

`[2(\cos 15+i\sin 15)]^3=8(\cos 15+i\sin 15)^3`

Now we will use the De Movier's Theorem that:

`(\cos \theta+i\sin \theta)^n=\cos n\theta+i\sin n\theta`

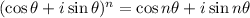
Hence, we have:

`[2(\cos 15+i\sin 15)]^3=8(\cos (15* 3)+i\sin (15* 3))`

i.e.

`[2(\cos 15+i\sin 15)]^3=8[\cos 45+i\sin 45]`

i.e.

`[2(\cos 15+i\sin 15)]^3=8[(1)/(√(2))+i(1)/(√(2))]`

i.e.

`[2(\cos 15+i\sin 15)]^3=(8)/(√(2))+i(8)/(√(2))`

i.e.

`[2(\cos 15+i\sin 15)]^3=4√(2)+4√(2)i`