Answer:
 +
+
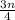 = n +1.
= n +1.
Number = 12.
Explanation:
Given : The sum of one-third of a number and three-fourths of the number exceeds that number by one.
To find : Which equation could be used to find the number.
Solution : We have given a statement
Let a number = n
According to question
One third of a number =
 .
.
Three - fourths of the number =
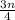 .
.
Sum of their is exceeds that number by one.
 +
+
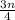 = n +1.
= n +1.
Taking common denominator
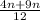 = n+1 .
= n+1 .
 = n+1.
= n+1.
On subtracting n both sides.
 -n = 1
-n = 1
Taking common denominator
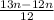 = 1
= 1
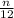 = 1
= 1
On multiplying by 12 both sides
n= 12.
Therefore,
 +
+
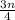 = n +1.
= n +1.
Number = 12.