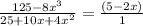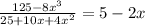Question

What is the quotient (125 – 8x3) ÷ (25 + 10x + 4x2)? –2x + 5 2x – 5 –2x – 5 2x + 5

Answer 1

The quotient is (5-2x)

Explanation:

Given the expression
`\frac{125-8{x}^(3)}{25+10x+4{x}^(2)}`

We have to simplify the above expression to find the quotient.

`\frac{125-8{x}^(3)}{25+10x+4{x}^(2)}`

⇒
`\frac{5^3-{2x}^(3)}{25+10x+4{x}^(2)}`

By the identity

`{a}^(3)-{b}^(3)=(a-b)({a}^(2)+ab+{b}^(2))`

Here, a=5 and b=2x

gives
`{5}^(3)-{2x}^(3)=5^2+5(2x)+(2x)^2=25+10x+4x^2`

∴ expression becomes

`\frac{125-8{x}^(3)}{25+10x+4{x}^(2)}=\frac{(5-2x)(25+10x+4x^2)}{25+10x+4{x}^(2)}=(5-2x)`

Hence, the quotient becomes (5-2x)

Answer 2

ANSWER


`\frac{125 - 8 {x}^(3) }{ 25 + 10x + 4 {x}^(2) } = - 2x+5`

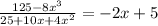
EXPLANATION

We have been given the quotient,


`\frac{125 - 8 {x}^(3) }{ 25 + 10x + 4 {x}^(2) }`
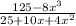
to simplify.

We need to rewrite the numerator as difference of two cubes.


`\frac{125 - 8 {x}^(3) }{ 25 + 10x + 4 {x}^(2) } = \frac{ {5}^(3) - ( {2x})^(3) }{ 25 + 10x + 4 {x}^(2) }`

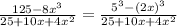
We need to make use of the difference of cubes formula,


`{a}^(3) - {b}^(3) = (a - b)( {a}^(2) + ab + {b}^(2) )`

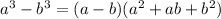
We now let,

`a = 5 \: and \: b = 2x`

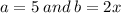
Then the numerator becomes,


`\frac{125 - 8 {x}^(3) }{ 25 + 10x + 4 {x}^(2) } = \frac{ (5 - 2x)(25 + 5 (2x) + {(2x)}^(2)) }{ 25 + 10x + 4 {x}^(2) }`

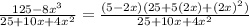
This simplifies to,


`\frac{125 - 8 {x}^(3) }{ 25 + 10x + 4 {x}^(2) } = \frac{ (5 - 2x)(25 + 10x + 4 {x}^(2)) }{ 25 + 10x + 4 {x}^(2) }`

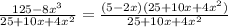
We cancel out common factors to obtain,


`\frac{125 - 8 {x}^(3) }{ 25 + 10x + 4 {x}^(2) } = ( (5 - 2x))/( 1)`


`\frac{125 - 8 {x}^(3) }{ 25 + 10x + 4 {x}^(2) } = 5 - 2x`