After dilating
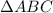 by a scale factor of 1.25 and rotating it 45° counterclockwise about point B, the side lengths of
by a scale factor of 1.25 and rotating it 45° counterclockwise about point B, the side lengths of
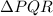 are PQ = 6.25 units, QR = 5.25 units, and PR = 5 units.
are PQ = 6.25 units, QR = 5.25 units, and PR = 5 units.
Let's denote the side lengths of
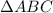 as
as
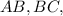 and
and
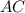 , and the corresponding side lengths of
, and the corresponding side lengths of
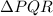 as PQ, QR and PR.
as PQ, QR and PR.
Given that
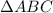 is dilated by a scale factor of 1.25 and rotated 45° counterclockwise about point B, we can determine the side lengths of
is dilated by a scale factor of 1.25 and rotated 45° counterclockwise about point B, we can determine the side lengths of
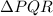 as follows:
as follows:
1. Dilating by a scale factor of 1.25:
-
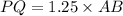
-
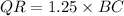
-
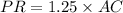
2. Rotating 45° counterclockwise about point B:
- PQ, QR, and PR are now the rotated side lengths.
Now, let's substitute the given side lengths of
 to find the corresponding side lengths of
to find the corresponding side lengths of
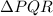 :
:
Given:
- AB = 5 units
- BC = 4.2 units
- AC = 4 units
Substitute these values:
1. Dilating by a scale factor of 1.25:
-
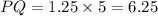 units
units
-
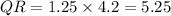 units
units
-
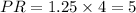 units
units
2. Rotating 45° counterclockwise about point B:
- The side lengths PQ, QR, and PR after rotation are the final side lengths.
So, the matched side lengths of
 are:
are:
- PQ = 6.25 units
- QR = 5.25 units
- PR = 5 units