Answer:
The diagonals of an isosceles trapezoid are congruent and the length of KM is
 .
.
Explanation:
Formula
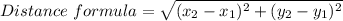
As given
The coordinates of isosceles trapezoid JKLM are J(-b, c), K(b, c), L(a, 0), and M(-a, 0).
The diagram is shown below.
Now find out the length of the diagonal.
As the diagonal is JL .
The coordinates of the JL are J (-b,c) and L (a,o)
Putting the value in the above
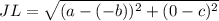

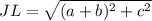
(As by using the formula(a + b)² = a² + b² +2ab )
Put this in the above
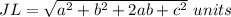
Now find the length of diagonal KM .
As coordinates of K (b,c) and M (-a,0).

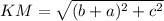
(As by using the formula(a + b)² = a² + b² +2ab )
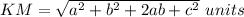
As the length of the diagonal JL and KM are equal .
Thus the diagonals of an isosceles trapezoid are congruent and the length of KM is
 .
.